そんな小学生はいないのかもしれない話
社会人学生として通った博士課程を今年2022年3月に修了しました.経緯なんかはこれまでのブログ*1*2を読んでいただけると幸いです.昨年の博士論文審査への山場(予備審査)までの日々なんかは前回ブログ*3にまとめたとおりです.要約すると,ユーリー先生に教官専用書庫の鍵をもらった,という話でしたね.そこから本審査(2022-01-17)直前の年末(メモをみると2021-12-22)になってやっとハッとなってシステムのアップデート案を思いつき,「出来らぁ!」などと言いながらシミュレーションを年末と正月にやって年明け早々工作室に詰めるものの結局は欲しかった実験結果は全部揃わず,考察を書き足すというところに落ち着きました.完全体ではないものの,指導教員の「なんかしらん間に実験システムめっちゃ変わってた」という評価もいただきながら,予備審査からのアップデートを本審査で評価いただき合格となりました*4.なんかかんやでそこからまたアップデートなんかもあり,2週間で出来らぁとか言ってたと思ったら結局1年かかってるけど?ないつもの感じで今はそのジャーナル論文を書いています(仕事の合間に).ここでは特にこの1年で研究とその周りの考え方について自分の中で得たものがあったのでそれについて書きます.
自分のやっている研究内容というのは光3次元計測であったり,3次元ディスプレイであったりと光線制御に関するものです.光線制御の方式はたくさんありまして,その中でも自分はレンズや鏡を使って,既存の方式だとうまくできないことをなんとかしますよ,というものです.ここで自分の中で薄らぼんやりと長らく引っかかっていた事があります.その研究,実はとても簡単なことなんじゃないの?という,特に誰から言われたわけでもないですがなんとなく思っていたことです.要は鏡の反射とレンズの結像/屈折なので,小学校の理科で出てくる内容です.実験のために必要な少し込み入った道具やノウハウなんかは別にして,提案手法の原理の説明だけなら小学生にも説明できて,理解してもらうのも可能だと思います.自分が小学校6年生だったときにはおそらく理解できないだろう要素が何個かあるなと感じるところですが,当時自分が通っていた日能研で教室前方に座っていたバケモノ達(当時その自分との差に驚愕した)なら少なくとも何人かはうんうんと説明についてくるだろうし,その後中学/高校/大学/会社に居たやべー連中なら,タイムマシンで小学生時代の彼らを連れてくれば確実に理解できるだろうな,と感じます.ここで研究は難しいものがいい,と言っているわけではないです.とはいえ小学生でも理解可能なこと,ということは上の年齢層まで合わせるとかなりの数の人間が内容を理解できるわけです.つまり,理解できる人が沢山いそうな(=取り組んだら出来ちゃう?)研究って,本当に価値があるものなのか,ということをずっと頭の片隅で在学中考えていました.これはここまで述べたような研究内容の理解のために必要な知識のレベル/量,という観点からもそうであるし,後述のように自分にとって研究が楽しくて仕方がなかった,という点にも起因していると思います.楽しいからやっていて,楽しいのは楽しいんですがそれが遊びや趣味といった概念と分類的に近くなってしまって,学問や知,専門性といった概念と離れているように感じていたからかもしれません.社会人博士という立場上どうにかこうにかやりくりしているこの貴重な時間とお金は無駄なんじゃないかとか,家のガレージで核融合炉を作っちゃうようなキッズが実は去年の自由研究でそれやったよおじさん?,とか言ってくるんじゃないか.そんなことを考えていました.
博士課程には結局4年半在籍して,各ジャーナル論文が採録になったときは自信を戻したり,研究がうまくいかなかったときは不安になったりしていたんですが,この1年で少し安定したというか,そんな小学生はいないんじゃないか,と思えるようになってきた,という話です.前置きがとても長くなりましたがこの記事は社会人学生 Advent Calendar 2022 - Adventar2日目の記事です.
おぼろげにつらつらとここまで書きましたが整理すると下記2点です.つまり「そんなん小学生でもできるで!」というツッコミと「そんな君は小学生レベルだよ?」というツッコミです.
- 研究内容が専門的知識なく理解できてしまえることへの不安.
- そんな研究をやっている自分の研究者/技術者としての力量への不安.
1番目の不安をそれとなく指導教員に伝えるとさすがの回答が返ってきました.要約すると,
深く細かく入り組んだところに入っていかなくても,少ない知識で理解できるレベルのところに問題をくくり出せて,その解決にもまた込み入ったことをしなくて良いってことは,それが価値になってるんじゃない?
これは良いことを言ってくれるなと思いました.基礎からちょこっと路地裏に入ったところに実は誰も通ってない道がふらっとあったりして,それがいい道だったりするかもなんですよね.簡単なことでも,それが今まで誰もやっていなくて,役に立つことなら価値がある.見つかっていなかったってことはなかなか気づく人も居なかった.気づけたことに価値があるんじゃないか.そうなんですよね.もうそこにあって,もう道筋ができてるからふんふんと理解できて,何気なく簡単に感じてしまうことってたくさんあるんですけど,ゼロの状態から作れってなったらかなり厳しい,いやいやこれ何食って生きてたらこんなの思いつくんだよ,ってなるものってたくさんあると思います.今ではもう当たり前になってしまってなんとも思わないけど,ミニ四駆でワーイとやったあとにRCカーを組んだとき,デフギヤ(特にボールデフ),ユニバーサルシャフト,Wウィッシュボーンサスあたりの機構に腰を抜かした当時の記憶が蘇りました.理解できる人が沢山いそう→取り組んだら出来ちゃうというのはそんな簡単につながるところではない,と思うことができました.
先生,ありがとうございます.
博士号取得後に学科の学生さん達に向けて博士課程の体験談を話す機会を頂き,色々なことを振り返ったりしていて感じたのが,自分は研究楽しめてやれていたなぁということです.上で述べたような不安っていうのは二次的なものというか研究の周囲に渦巻いてるものなんですが,その研究の中心でやってる手を動かしてシミュレーション組んだり実験したり,ってのは楽しくて仕方がないです.そもそも博士課程進学にあたって理由ってその学位だったりその後のキャリアパスだったりと人それぞれかと思うんですが,自分の場合はこの研究やってる時間楽しいんす!というのが1番大きいです(入試のときには楽しいは楽しいけどそこまで本当に楽しめるかまだちょっと自信はなかったですし,楽しいからっす!!!っていう説明はさすがにヤバそうなのでそれは避けて新規性やら有用性なんかを言いました).小さい頃から工作したりミニ四駆したりプラモデル作ったりするのが好きで,その感覚に近いなと思います.仕事終わりや休日に研究して偉いね,みたいなことを言っていただけることがあります.時間を作るという点ではかなり頑張ってはいましたが,自分の中ではTAMIYAプラモデルファクトリー*5に行っているような感覚なのでちょっとそこは苦笑いだし,いやむしろ夫が大学という名のミニ四駆屋に入り浸ってるのに許可出してくれる妻氏&子ども達の方が偉いのでは...でもまあなんか俺とりまツイてる?と思っていました.もしかしたらそんな感じなので上のような不安があっても平気だったのかもしれません.妻氏におれの趣味って自転車とボルダリングとあと何かある?って訊いたら即答で「大学」と返って来ました.この,楽しいと思えることを見つけられた,+気付くことができたというのがここで言いたかったことです.楽しく感じることと,合ってること(結果が出るか?)というのは別の問題でもある(下手の横好き)んですが,「楽しいと思えること」が合ってることの一要素でもある(好きこそものの上手なれ)と思います.考えてみれば集中力は他のことに比べて明らかに高いですし,別のことをしていてもなんとなくそのことを頭の端のほうで考え続けていられます(自分調べ).自分は小学生から高校生までサッカーをやってたんですが,今から思えば楽しめていなかったんだなと思います.反対に大学から始めた自転車はとても楽しくできて,これは自分のフィジカルやメンタリティと相性が良かったこともあるんですが上手くマッチして結果も出ました.楽しいとトレーニングも集中できるし効率が全然違うんですよね.大学入試,専攻選択,院試,社会人経験など経て30過ぎでやっと進路が少しクリアになりました.耳をすませばの聖司くんはあの年齢で進路をバッチリ決めていて本当にすごいですよね.自分はかなり時間はかかりましたがそういうものをやっと見つけられた気がしています.また,進路選択を今からでもできる環境にも感謝だなと思いました.たぶん自分が楽しそうにやってるのを見たからか,妻も今年から大学に入学してます.
さて,指導教員のありがたい言葉で1番目の不安が消え,楽しいと思えることに気づいて2番目の不安要素も薄れてきました.あとはこのテーマが本当に自分に合ってるか(下手の横好き疑い),という点です.ここで自分の中で,学位という一つの形になった,ということがかなり大きな支えになったように思います.もともと自分は謎の自己肯定の習性があって,例えば数式ハラスメントな授業(自分がそう感じていただけです.すみません)で心がやられちゃいそうになっても「いやいや先生の板書の理解全くついていけなくなってるけど,いうてこの教室の中で個人追い抜き(自転車でやる4kmのタイムトライアルです)一番速いのワイやん?」という謎の論理を以て自分の形を保っていました.こんな自分にとって,なかなか博士号はいい鎧になります.人から何を言われようとも(繰り返しになりますが人から非難されたことはないです),あの先生方が認めてくださったんだからへーきへーきとなりますのでかなりメンタル的に助かります.ということで博士号も取れたしこのテーマ,合ってるのでは?いやいや,合ってるでしょ!
そんなこんなでいい指導教員に巡り合って,楽しくやって,学位もらえて,ちょっと自信ついたよ.という社会人学生おじさんの話でした.
縁あって今はアメリカで仕事しているんですが,同僚から「これ子供の自由研究やねんけど君の研究テーマと似てない?」とかスマホの画面見せられて気絶する,ということも幸いまだ経験ないです.
社会人博士課程近況報告
(こちらは社会人学生 Advent Calendar 2021 - Adventarの3日目の記事です.)
今年も書かせていただきます.改めて自己紹介いたしますと,東京大学大学院情報理工学系研究科の博士課程学生です.2017年9月入学ですので現在5年生となってしましました.社会人的要素の方は日立製作所研究開発グループで人工知能イノベーションセンタなるところに所属しています.ご参考*1(なんかテクノロジーによってちゃんとした感じの青年風ですね.これが私の真の姿ですのでよく覚えておいてください).
いろいろ大変だったけど,どうやら来年2020年3月修了(4年半)で博士号とれそうな雰囲気出てきたよ,というのが概要です.
去年の同時期に書いた内容*2からやっていたことですが,なんとかまずは2本目の論文を通した,というのが最初の話題です.去年の12月の段階でまあほとんど書けていたので,英文校閲などをはさみながら1月には投稿できました.んで2月に結果が返ってきてリバッタルです.ここでありがたかったのが緊急事態宣言のことを学会側に説明するとすんなり修正期限を延長してもらえたことです.神です.論文誌としてはかなりのスピードで審査してもらえるこの論文誌*3ですが,レビュワの方々にこのスピードで審査していただきながらこっちの修正遅いってちょっとだめなやーつやん…とか僅かに思いながらもちょうど仕事も忙しかったのもあってお言葉に甘えてしっかり時間をかけて修正しました.その後は3月修正稿提出と回答,4月採録となりました.万歳.このテーマには正直時間をかなりかけてしまって,設計ミスをやらかしてしまったり,一度装置を組んだけど組立精度が出なくてもっと精度高いパーツで組み直したり,曲面鏡の制作で表面蒸着メッキについて学んで神がかり的に親切で腕のいい職人さんに巡り合ったり,,など色々ありましたが,論文書くぞとなってからはすんなりで良かったです.あと,博士論文への貢献という意味でもとても大きな前進でした.うちの研究科の博士課程では博士3本柱と言われていて,業績が3つ必要と言われています.業績というのは学会発表でもいいし,なんなら学会には通っていなくても実験結果だけでもなんとかなるらしいです.とにかく博士論文審査で先生方がそれぞれが1つの柱となるべき内容になっているかをみるというものらしいです.ですがまあディフェンスのときに論文通ってます(フンス!!)と言えるのがベストなので,ここで2本目の論文がすんなり通ったのは非常にデカイです.
次は娘氏が3月に生まれたよ,という話です.思えば大学入学した頃には妻氏と自分の二人暮らしだったんですが,2018年に息子氏が登場し,今年には娘氏が登場しました.振り返れば2017年当時いろいろありましたが思い切って進学を志してよかったなと思います.たとえば今の現状から新たに進学,というのはだいぶ心理的に超える壁が大きい気がします.話を戻すと,娘氏の登場に合わせて会社は育休取得しました.娘氏は3月の下旬に登場したので,3月の下旬-5月の下旬まで育休,5月の残りは有給休暇で休みをもらい,2ヶ月と10日くらいの長い休みをもらうことができました.なんで期間中途半端だし有給使ってんの?というところは,私の自治体のルールが「父母同時に育児休業を取得する場合は、保育の必要性が認定されず、先に通園している保育園を退所となります。(要約)」となっていて,これ以上育休とると上の息子氏が保育園にいけなくなってしまうためです.このため妻の産休終了(育休開始)の日までしか自分の育休は取れませんでした.育休期間中は2人目ということで慣れた部分もあり勝手知ったるで楽にこなせるところもあれば,想定外のこともあったりでかなり慌ただしく育休期間を使い切りました.新型コロナのこともあり実家の両親を招聘するのも難しかったですし,この育休無かったらどうしてたんかな...となるような感じだったので非常にとってよかったなと思いました.育休取得はじめ関係者の皆様には感謝の限りです.改めてありがとうございました.こんな感じなので大学の方で3,4,5月は進捗なしです.
次は博士論文3つ目の柱となるテーマの話です.上のような感じで6月から本格的に作業再開したわけですが,一応去年から論文投稿の裏で実験装置の設計やらシミュレーションやらをやっていたのでゼロからというわけではなく,6月時点で装置の大体ができていた,という感じです.6月7月はある程度構想を練っていた内容のために装置のキャリブレーションやって追加の実験装置作ってデータ取って...ということをしていました.そんなこんなしてるうちに新型コロナが結構なやばいことになってきてしまって,大学に実験で出るのがちょっと...という感じになってきます.学生時代みたいに大学まで徒歩圏内だったりすれば特にためらいは無いんですが,まあまあ混んでる電車に乗って通学が必須とかだとちょっと悩みます.ワクチンは幸い同世代の中では早い時期に2回目まで完了できていたんですが,この辺のリスクテイクのバランスは人によると思います.結果8月は完全引きこもりにしました.幸い上で述べた実験,と言ってもまあ予備実験くらいの感じなんですが,7月の末に指導教員とこれをポスターに出そうかという話をして,8月頭にはこの投稿内容を書こう,またこの内容のブラッシュアップ(サーベイとかストーリー作りとかこれからやる実験案)を8月後半にやろうということに決まり,大学には行かなくて実験もしないけどそれなりにやることはある,という感じで8月は過ごします.正直この段階では,来年の3月終了は無理かな〜という感じになっていて,大学に行く通学時間がなくなったことでできた時間なんかで余裕ぶっこいでこんなの*4を書いたりしてました.シン・エヴァ良かったですね.とかなんとかしてるうちに8月も終わりになって,再度指導教員と打ち合わせです.自分は長期履修状態ですので半年ごとの3月と9月に,次の半期で博士論文審査のトラックに乗るかやめるかの返答を教務課にする必要があります.ここで指導教員にこうこうこういう状況でやんすけど,まだまだ材料足りんすよね…ちょっと今回も見送りかなと…みたいな空気で相談したところ,
指導教員「え?そうなん?ポスターも出せてるし,内容的にも9月にもうちょい頑張ればイケるで!!!(意訳)」
なるコメントをいただきます.お,おう…でもそんな頑張るような感じで大学行けるかいな???と思うもののこの追い風は嬉しいです.妻氏に相談してみたところ
妻氏「え?そうなん?じゃあさっさと卒業せえや!!!9月は好きなだけ大学行ってええで!!!(意訳)」
なるコメントをいただきます.お,おう...っしゃーおらー!!!!!であります.まあ状況をわかりやすく説明すると,キートンがユーリー先生に教官専用書庫の鍵をもらった状況とほぼ同一です.本当に協力してくれた家族に感謝です.ということで9月は本当に会社の業務以外の時間全てフルコミットで大学にぶち込みました.通常の1週間で大学の方にかけられる時間は20時間くらいなんですが,この9月中は1日の飯・風呂・睡眠以外の16時間の内,平日8時間の業務以外はすべて大学のことに使えたので1週間で72時間くらい使えます.時間だけみても3.6倍ですが実機を動かしての実験なんかはまとまった時間があるとその分捗るので実際この1ヶ月で半年分くらい進みました.今思い返すと,あ〜9月は時間もかけられたし進捗も出たし充実してたなぁ〜という思い出なんですが,よくよく考えてみると当時はうまくいくかわからん実験や理論整理なんかで結構きつかったです.あとは9月末で実験室を引っ越ししないといけないというバタバタなんかもあり,なんとか完走したという感じでした.あと嬉しかったのは上でちょろっと述べたポスターに通ったのも大きかったです.新規性の主張が結構微妙な気がしていて,指導教員ともそんな話をしていたんですがなかなか高評価でアクセプトだったのでこれはテンション上がりました.
最後に博士論文審査の話です.上のような感じで怒涛の9月を終え,9月末に再度指導教員と打ち合わせて来年3月修了に向けて審査を受けることになりました.大体うちのコースではこのトラックだと11月中頃予備審査,年が明けて1月中頃に本審査です.11月中頃予備審査にはもちろん説明資料も用意しないといけませんし,事前にだいたい1週間くらい前には審査いただく先生方に博士論文を送付する必要があります.9月が上のような感じでてんてこ舞いですってんてんだったので,もちろん10月頭の時点で博士論文も説明資料もこの世には1バイトも存在していません.学部時代の同期でもうとっくに博士号とった奴と話してたら1ヶ月で間に合うんかいなみたいなこと言われました(まあこいつは定期テストに計画的に準備して臨むタイプですが).それどころか上のポスターの方で学会に提出する動画を撮らなきゃいけなくなったものの,引っ越しで装置を1回ばらしてしまったため組み直し+再度キャリブレーションが必要になりました.さらにキャリブレーションが8時間かかる上に途中で結構大きめの地震があってもう一回やり直したりしてかなり時間を削られました.なんやかんやしていたら大体書くことの箇条書きメモ程度は10月第1週には書けていましたが実際にちゃんと書き始められたのは10月第2週からです.予備審査の日程は結局11/12と決まり,この1週間前11/5が博士論文自体のデッドラインです.図をちゃんとしたり引用を合せたりなどの調整に1週間かかると見て10/29には少なくとも博士論文の形をしたものができていないといけません.1章の序論,2章の背景はちゃんと時間をかけないといけないなと言う意識はあり,一方で3本柱の各論となる3章4章5章にはそれぞれ投稿済みの論文と9月に整理した内容をあてればいいとはなんとなく考えていました.結局1章の序論にまるまる1週間,2章の背景をなんとか3日で終わらせました.ここで10/20水曜日です.この時点で博士論文そのものが20ページくらいしかない状況はかなり焦りました.ですが各論に入るとサラサラと書けて,結局ちゃんとなりました.とまあかなりカリカリしながら書いたような雰囲気を出してますが,実際書いてるときは楽しかったです.自分の好きな分野の概観なんかを色々もう一度調べながら書く,というのはなんでしょうね世界史資料集をずっと眺めてられるような面白さがありました.さて11/5金曜日に博士論文を先生方にお送りしたと思ったら次は発表資料です.もちろん11/5の午後先生方にメールし終えた時点で「予備審査.pptx」はこの世にまだありません.なんか自分でもよくわかりませんが勢いと過去の学会発表の資料などの助けを借りながらなんとか予備審査当日11/12の朝までに完成にこぎつけました.これほど学会発表しといてよかったと思ったことは他にないです.論文投稿だけにしなくてよかった.発表時間50分の内容なので練習はあまり回数はできませんでしたが早起きしたりなどして再度練習をやっておいて,当日朝息子氏の「とうちゃん頑張ってね〜」で勇気をもらいました.発表自体はなんとかうまくできたかな,という感じでしたが,オンラインだったので途中の先生方の雰囲気が読めずかなり脂汗をかきながら話していました.質疑も後から指導教員と振り返れば粗がありましたがベストを尽くせたんじゃないでしょうかという感じで無事終わりました.結果,終了後20分ほどで合格のご連絡いただきました.とりあえず休まねばということでずっと行きたかった庵野秀明展に行き,寿司を家族と食べて*5寝ました.
かなりドタバタとしてしまった3ヶ月でした.精神と時の部屋に入ってた感があるので9月がもう1年くらい前に感じます.もちろん,計画的に準備しなはれ!時間に余裕をもって!というご意見はごもっともなんですが,えいやっとこの短期間で集中してできたのはよかったかなと自分では思いました.例えば自分は文章を書くとき,紙にペンでザザーと下書きをしてから書くんですが,今回は序論を書いている段階で「こんなことでは間に合わん!!」となってもう直接texに打ち込んでいきました.いままでは一回紙に書いてじゃないとまともな文章は書けんのや,と思い込んでいたんですが直接アウトプットでもいけることに気づけてよかったです.いやすみません,いけてるのかは結局わからんですが予備審査合格なので許してください.本審査までにはちょっと時間があるので,ここで時間をかけて上げられるところを上げていきます.要するに集中できてよかったですということが言いたいです.
去年こんな記事*6
エジソン ひどいのは社会人博士。3年間毎年53万円払えば博士号を取れる。下手したら指導教官に論文を書かせて博士の肩書だけもらえる。教授の判断で短縮卒業だって可能。
(https://www.newsweekjapan.jp/stories/technology/2020/10/post-94727.phpの3ページ目より)
を見かけて,「え,そうなん???いやいやいや...というかむしろ社会人博士の印象ってこんななん...」となってちょっと悲しくなりました.ですがまあ色んな人と話したり,研究しながら考えたりして,結局のところ自分がちゃんとしようとなったこの1年でした.こんな記事が存在するということは,ここにあるような例や近い例も存在するのかもしれません.まあでもそんなことは気にせず胸を張って博士号とったぜ!と言えるような頑張りをして,ほんとに君博士号持ってんの?と思われないような頑張りをし続けて行こうと思うのでした.
本審査がんばります.良いお年を.
*1:https://www.hitachi.co.jp/recruit/hrsystem/stories/05.html
*2:https://yasutchi.hatenablog.com/entry/2020/12/05/074917
*3:https://www.osapublishing.org/oe/home.cfm
*4:https://yasutchi.hatenablog.com/entry/2021/07/31/084956
*5:https://twitter.com/Yasutchi/status/1459105380210921472
*6:https://www.newsweekjapan.jp/stories/technology/2020/10/post-94727.php
庵野秀明監督のカメラを追う
タイトルの通りです.以下のツイートにある,庵野監督によるカメラの動きを再現していきたいと思います.
【制作こぼれ話】イメージしている実写の手持ち風カメラワークを表現するため参考にすべく、モニター画面を総監督自らiphoneで撮影。
— (株)カラー 2号機 (@khara_inc2) 2021年7月15日
これらから、一番イメージに近いカメラワークを選び、コンポジット時に再現
※暗いモニターに反射で映るのは庵野総監督ですが、途中でふいに誰か来ます#シンエヴァ pic.twitter.com/COKG2zqMzQ
カメラの位置姿勢推定については,カメラの内部パラメータとカメラの外部パラメータを求めることで可能です.内部パラメータは,庵野監督がiPhoneを使用しているという情報から求めていきます.外部パラメータは,別のツイートにもあるように,モニタ上の黒点は100mmごとに打たれた格子点とのことなので,この情報を使って求めていきます.
まず,内部パラメータの推定です.これはカメラの焦点距離や歪みなどの情報です.パッと調べた限りiPhoneの型番ごとのカメラパラメータが公開されていないっぽい(されてたら教えて下さい)というのと,swiftをいじればわかるっぽいんですがswift完全素人なので自分で推定するところからやることにします,監督の使用されているiPhoneと同じものを用意できればいいんですが,あんまりiPhoneのバリエーションに詳しくないので,ここは自分の持っているiPhoneと同じものを使っている,ということにして話を進めます(「プロフェッショナル仕事の流儀」でも使用されている姿がよく映っていたので詳しい方,わかれば教えて下さい.というか数値そのものご存知でしたら教えて下さい).いきなり監督のiPhone=自分のiPhoneというクソデカ仮定を置きましたが,まあスケールとか歪みとかがズレるくらいだろうということで気にせずいきます.
定番アイテムのチェッカーボードを使って,内部パラメータ推定を行います.といっても,Fig. 1のようなチェッカーボードの画像を何枚も撮って,OpenCVのcalibrateCamera関数に放り込むだけです.ここでの注意としては,iPhoneは写真撮影と動画撮影とで画角が変わってしまうので,ちゃんと条件を合わせるために動画で撮影します.今回は動画で撮影した後,適当にその中から画像形式で抜き出して先の関数の入力としました.

次に,外部パラメータの推定です.これは,世界座標系における座標やベクトルをカメラ座標系での座標やベクトルに変換する回転と並進の情報です.Fig. 2に位置関係を示しました.ここでまず最初に世界座標系を決めなければいけないんですが,先述のモニタ上に配置された黒点を使います.画面横方向に軸,縦方向に
軸,画面と垂直でカメラのある方向に
軸をとり,ちょうど水面から顔を出したマリの頭と重なる黒点を原点
として定めます.
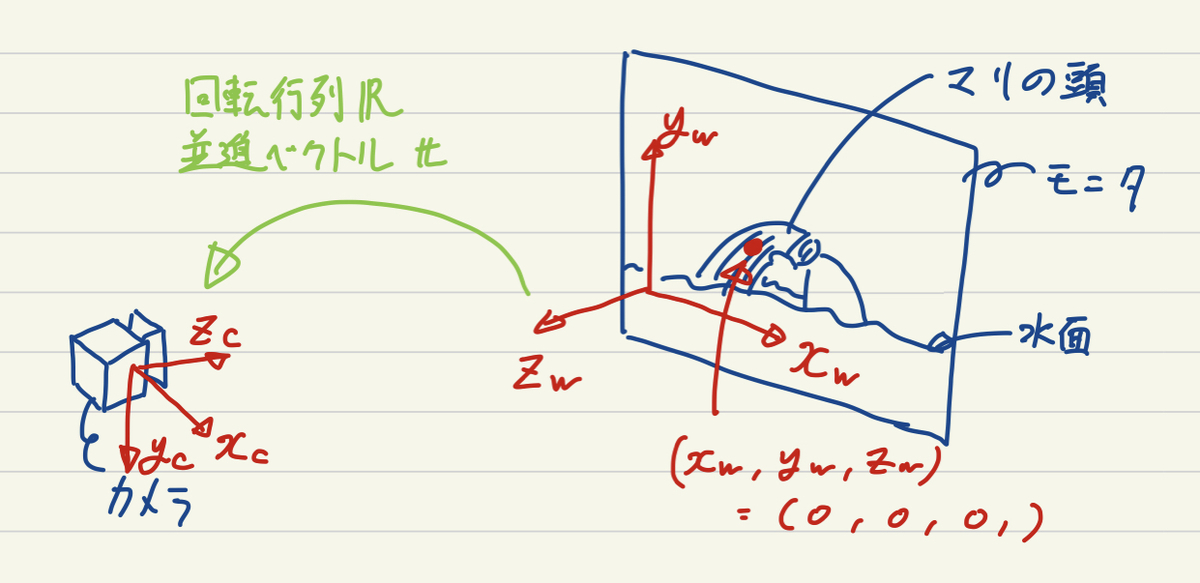
カメラの画面内に世界座標上での位置が既知な点が4点以上あれば,カメラの位置姿勢を求めることができます (PnP問題).つまり,動画の各フレームで4点以上の黒点を検出し,それらがカメラ画像中でどの位置に写り込んでいるか,それらが世界座標系においてどの位置に配置された黒点か,を求めていきます.これらが分かれば,OpenCVのsolvePnPRansac関数とRodrigues関数を使って,回転行列と並進ベクトルを求めることができます.ここで求められた回転行列と並進ベクトルは世界座標系における座標やベクトルをカメラ座標系での座標やベクトルに変換するものなので,今回のようにカメラの位置姿勢が欲しい場合には下の式のように,逆行列を用いた式変形を行った後,カメラ座標系における位置を代入することで位置が求まります.
カメラの姿勢については世界座標系におけるカメラの方向ベクトルを求めたいので,下式にカメラ座標系における方向ベクトル
を代入することで求めることができます.
さて,ここからはどのようにして動画の各フレームで黒点を検出するかです.そこまでフレーム数も多くはないので,チクチクと手作業でもいいんですができるだけ自動化してやっていきたいと思います.単純に二値化して黒い部分だけ抽出してもトレス線なども引っかかってしまうためうまくいきません.特徴点マッチングなんかもあんまりうまくいきそうにないので,今回は最初のフレームだけ各点の初期位置を登録して,それ以降のフレームでは前フレームの黒点位置の周囲のみを探索するようなトラッキングっぽい手法でやっていきます.Fig. 3に示すように,現在のフレームでの黒点位置は前フレームの黒点位置の周辺に来るはずです.なのでこの周辺範囲内でなら,黒点以外の余計なものが映り込む可能性がガクッと下がるので二値化処理でかんたんに黒点を見つけることができます.
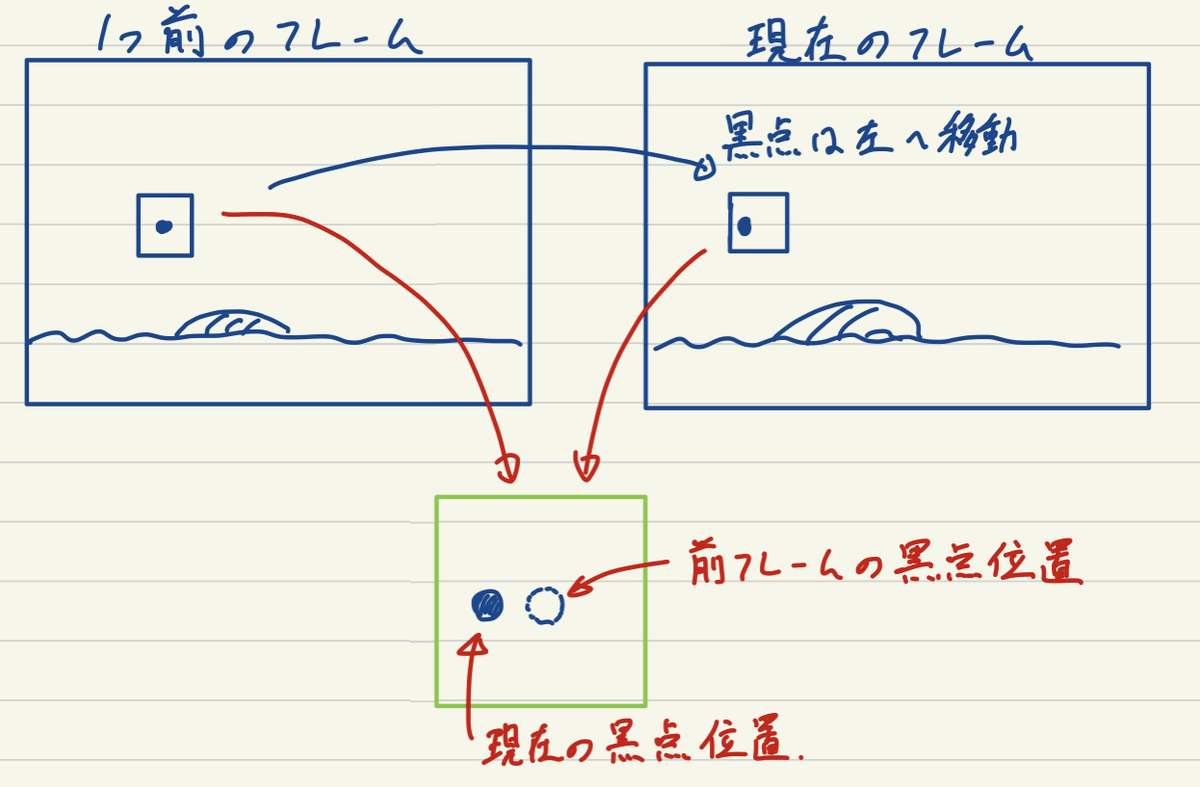
ただ,このままだと最初のフレームに映っている黒点しか見つけられないので,この動画のように最初のフレームでは映っていなかった黒点が画面内に出て来るような場合に,これらを検出できません.そこで,一旦求めた現在のフレームでの外部パラメータを使って,見つけられている以外の黒点がカメラ画像平面でどの位置に来るかということをOpenCVのprojectPoints関数を使って再投影計算していきます.これによって,発見できていない黒点のカメラ画像中での位置が例えばのように画角以外の場所であれば無視してOKですが,画角内部に収まるような場合にはこの周囲も同様に探索し,初めて画面に現れたような黒点も検出します.またこれによって,マリの頭と重なってしまいこの間検出できていなかった黒点もその後復活して検出できるようになります.
以上の手順によってカメラの位置姿勢の軌跡を計算できます.と言いたいところですが,実際には検出を間違えたところの補正を手作業でやっておりそれなりに疲れました.モーションブラーが乗ると黒点の黒が薄まって二値化がうまくいかなかったり,黒点とトレス線が非常に近い場合にもうまくいきませんでした.とはいえすべて手作業と比べたら断然楽です.
Fig. 4に1カット分のカメラ軌跡を示します.この動画中でマリは10回水面から浮上しますが,ここに示した結果は一番最初に浮上したカットにおけるカメラワークです.青で示した折れ線がカメラの位置の遷移で,青点が各フレームでの位置です.赤線で示したのがカメラの向いている方向です.画面横方向におよそ150mm,画面縦方向におよそ100mm,画面から離れる方向におよそ300mm移動していることがわかります.カメラの方向はほとんどモニタ画面に対して垂直ですが,位置の遷移とともに微妙に変化していることがわかります.
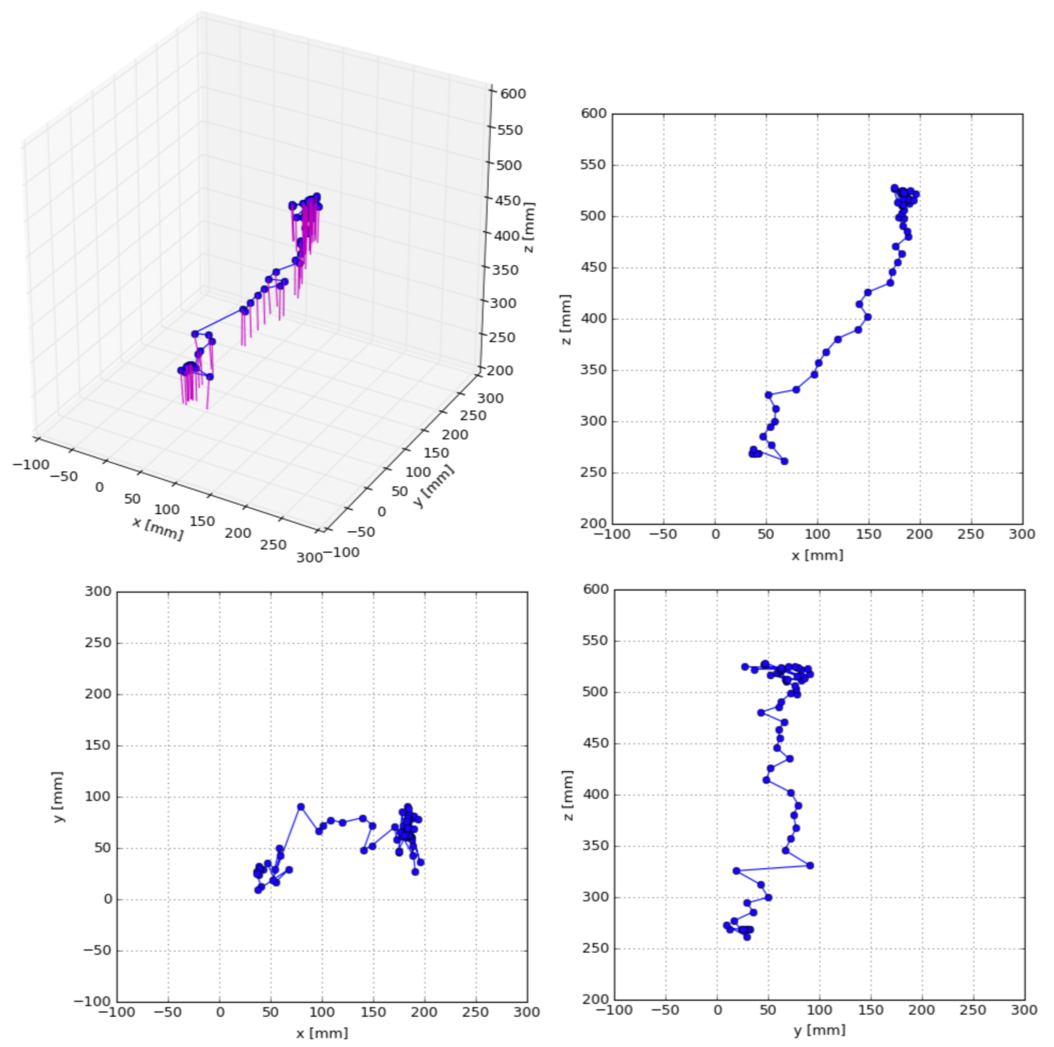
Fig. 5に3カット分のカメラ軌跡を示します.上で合計10カットあると述べましたが,2番目と3番目のカットでは最初のフレームでカメラがモニタ画面に近すぎるため映り込んでいる黒点の数が十分でなく候補から外しました.また,5番目と7番目のカットではタイミングを図るためにカメラは動いていません.故に,前から使えるカット3つ分ということで,1,4,6番目のカットを使っています(8,9,10番目については時間の関係上検討していません).3つを比較しても再現性高くほぼ同じ軌跡を描いていることがわかり興味深いですね.
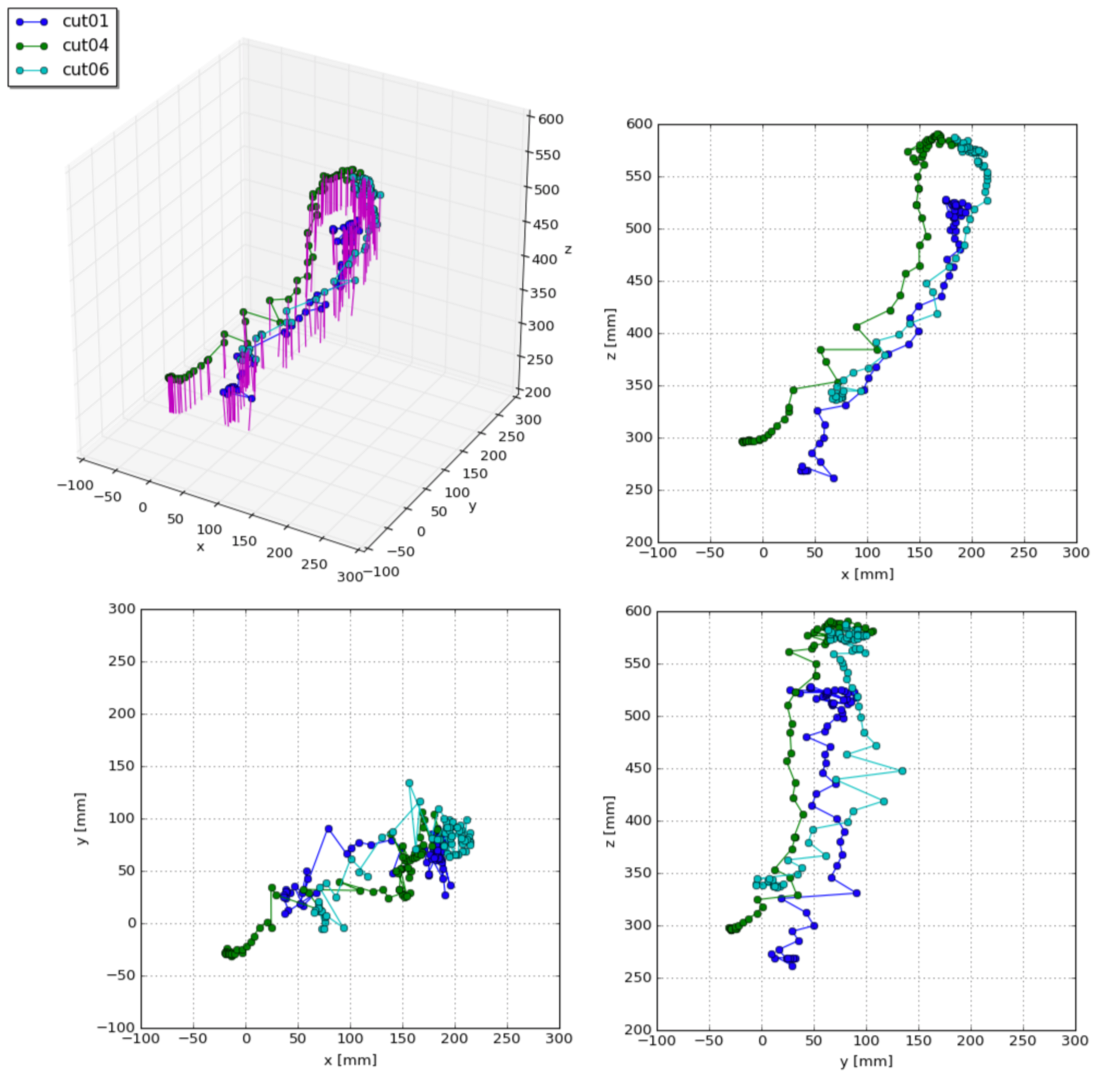
ということで最初に述べた,庵野監督によるカメラの動きを再現,ができました.
もっといい方法があるぜ!とかのご意見や,実はカラー内部ではこうやっていてですね...といった極秘情報などお待ちしております.
参考:
カメラキャリブレーション — OpenCV-Python Tutorials 1 documentation
姿勢推定 — OpenCV-Python Tutorials 1 documentation
1年前の自分へ
(こちらは社会人学生 Advent Calendar 2020 - Adventarの5日目の記事です.)
1年前の自分へ
この文章を書いているのは2020年12月5日のお前だ.
この10月で博士課程4年生になった.ああ,そうだ4年生だ.気を落とすな...気持ちはわかる...3年では無理だった.そして来年2021年春でも無理そうなので2021年の秋修了を目指して頑張っているところなんだ.
いいか,お前にとって来年2020年は色々大変な年になるから心しておけ...ここにそのためのアドバイスを残すから参考にしてくれ.
お前はいまやっているシミュレーションもなんとなく上手くいっているし,後は実験装置組み上げてデータとって,4月くらいには論文出るなーとか思っているだろう.甘い!!!甘いんだよ...よく聞け,いま自分がこの文章を書いている2020年12月5日の時点で論文はまだ出ていない.ああそうだ...出ていないんだよ......
大きな理由は3つだな.
・新型コロナウイルス
・シミュレーションバグ
・キャリブレーションうまくいかない
じゃあ2020年を時系列順に説明していく.
1月:シミュレーションの結果を反映した試作品が出来上がる頃だな.実験装置の例の部分の作り方だが今手元に2案あるだろう.それな,手間のかかる方の案があるな,それでやれ.1つ目の案だと誤差が大きくて使えないんだ.なんとなーくうっすら勘づいていると思うが,やっぱり出来るだけ頑張る方法じゃないとダメ.1つ目の案をまず試した結果のこの試作品だが,結果これは使えなかった.
2月:サンフランシスコ開催の学会に行く*1.これはいい感じに出来る.準備もうまく出来るし,トラブルもない.展示も面白いし色々見て回れ.メーカーの人とも色々話せ.アルカトラズ島の見学ツアーは超おすすめなので絶対に行け.ハンバーガーとルートビアがうまいぞ.次のテーマのアイデア出しもあるからここでいろいろ考えておけ.
3月:このあたりから新型コロナウイルスというのが流行り始めていろいろ状況が怪しくなってくる.会社は基本的に在宅になる.ちなみに現時点の2020年12月でも在宅勤務中でこれは本当にありがたい.
いよいよ実験に着手するんだが,先に言ったとおり1つ目の案で作った試作品だと誤差があるから思い通りの実験ができない.結果も出ない.でもここでいろいろ試行錯誤したのは後々役に立つ.ああ,あと...3月な...ノートPC,「壊れるかもしれないけどこれ試してみようかな...」とか思うことするなよ?絶対にするなよ!!!いろいろ世の中が大変な時期にハードからの復旧は本当に大変になるからな!!!
4月:緊急事態宣言とかいうアニメとかでしか聞いたことのないような名前の状況に世の中がなる.基本的に外出が出来なくなる.家でゆっくり仕事と大学の事出来る〜とか一瞬考えてるだろうがそうはいかない.お前のもうすぐ2歳になる息子の保育園もせっかく4月から始まったと思ったら1週間で休園になるぞ.これがどういうことか.以下の時間割を見てくれ.
6:00-7:00 息子氏起床→自分も起床
7:00-8:00 朝ごはんとアンパンマンたいそう3セット
8:00-10:00 息子氏とプラレール→公園
10:00-12:00 妻と交代して在宅作業
12:00-13:00 お昼ごはん
13:00-15:00 在宅作業(息子氏昼寝)
15:00-17:00 息子氏と公園orプラレールor在宅作業(妻と交代)
17:00-19:00 お風呂,晩ごはん
19:00-20:00 アンパンマンたいそう3セット→息子氏は就寝
20:00-24:00 在宅作業
24:00-25:00 就寝
つまり自宅保育になり,同じく在宅勤務の妻と交代で息子氏と遊ばねばならん.息子氏の起きている間は必ず自分か妻が息子氏にマンツーマンディフェンスしないといかん.あと言っておくが一日中家でプラレールなんてのはだめだ.絶対に夜寝ない.雨が降っても公園にお散歩に行け.心配せんでも息子氏は行きたがるのでお付き合いするだけでいい.そして息子氏に少しでもお遊び疲れいただくのだ.そろそろ大人の速歩きじゃ追いつけない機動性だろ?もう一緒に外で遊ぶそれだけで大人はくたくたになる.日中にできる作業は限られると思ったほうがいい.寝食を忘れてコーディングなんてことはもう絶対できない.自分の体力を最大限残しつつ息子氏に夜ぐっすり寝ていただくラインを見極めろ.緊急事態宣言自体はGW明けに解除になるが,5月いっぱいまでは登園自粛期間なので2ヶ月間この生活になる.心して臨め...
もちろんだが大学も行けなくなるぞ.あと,もともとやっていたシミュレーションにバグが見つかる.あの気づいた瞬間にすーっと血の引く感じは本当に良くない.これを防ぐために何ができたかというと結構難しくて,もっとコードテストの勉強をしておけばよかったのかな,くらいしか無い.ユニットテストは通る系だったので結合のところで気を抜いていた.どうかお前は気づいてくれ.このせいでだいぶ巻き戻ってしまう.この件もあるし,大学にも行けないしなので,コードのリファクタリングと実験の組み直し,あとは関連する分野の勉強をすることになる.
5月:もういろいろキツくて記憶がないんだが,今メモを見ると実験装置の例の部分の作り方,やっとここで2つ目の手間のかかる方の案でいこうと決めているな.それでいい.あとはこのタイミングで実験装置全体の設計を十分時間をとってできたのが良かった.結果,組み上がる実験装置はいい出来になった.
もう日中は息子氏との外遊びに全振りしているからサングラス*2なんかを作っちゃう.めちゃくちゃ良かったので早く買え.
6月:このあたりで9月頭の特集号を狙うようなスケジュールを引く.息子氏の保育園が再開となる.保育士さんたちには最大限の感謝をしろ.圧倒的感謝で臨め.
息子氏が日中保育園に行くので時間はできるが,ここまでの2ヶ月の借金で仕事が忙しくなるのと,実験装置の一部を自作できないかな?とかいう,結果的に時間を無駄にする検討を挟んでしまい,あまり進捗がないまま1ヶ月が溶ける.自作できると試行錯誤のプロセスが楽にできる点は良いがクオリティが落ちる.今回はクオリティが大事だったからプロに任せたほうが断然良かった.
7月:このあたりからキャリブレーションが収束しない問題にぶち当たる.そう,最初に上げた遅延要因3つの内の3つ目.実験結果とシミュレーションのすり合わせが収束しない.原因は2つあって,最終的にそれに気づくのは1つ目が8月頭,2つ目が8月中旬になる.それまで本当にいろいろ試すもうまく行かなくて心が折れる.1つ目はアルゴリズム的な工夫で解決できて,2つ目は設計を少し近似でやってるところを厳密に直せば解決できる.頑張って早く気付け.息子氏に「なんでキャリブレうまくいかんのかな???」とか訊くといい.ヒントになる単語を口走る.
新型コロナウイルスの前はボルダリングで身体を動かせていたが,そうはいかなくなる.会社にも行かないので昼休みの懸垂もできない.屋内自転車ローラー環境を整備しろ.自分は7月にスマートローラー*3を買ってzwift環境を得たが,もっと早くてよかった.数年悩んでいた腰痛も消える.早く買え.
8月:大学に出られる環境が少しづつ整い,ちゃんと実機実験ができるようになる.いろいろ実験してやっとキャリブレーションがうまくいく.最終的な実験もうまくいく.だがちょっと遅すぎて目標だった9月の特集号には間に合わない.
9月:半期の締めだから仕事が忙しくなる.もともと僅かな隙間でやっている学生生活だからちょっと仕事が忙しくなると時間がなくなる.修士の頃だったら2日位かければサクッとできたことに平気で1ヶ月かかったりする.あと,さっき言ったzwiftだがな,あんまり追い込むと体調を崩す.いい汗かいたな〜くらいでやめておけ*4.
10月:データ取りなどなどしていたら論文の第一稿が仕上がったのが10月中頃になってしまう.月の後半は新テーマのための予備実験の予備実験みたいなことをやってデータを取る.あとはその環境構築に1日くらい使う.
11月:なんやかんや論文の添削やり取りを指導教員としていたら1ヶ月経つ.新テーマのシミュレーションもちょこちょことできるがあまり進捗が出ない月になる.ちょっと気が緩んだ週があって,「俺の魂がやる気になるのを待つ」*5とか言っていたら数日溶かした.やれ!締切が先だからとか言って寝かしておくと間に合わなくなるぞ!やれ!!いいからやれ!!!手を動かせ!!!
...という感じ.
冒頭でまだ論文は出ていないと書いたが,いちおう投稿寸前のとこまでは来ている.そこは安心してくれ.
では健闘を祈る.
点と直線の距離計算
メモ
def line_point_dist(line_p1,line_p2,point): #line_p1:直線上の一点 #line_p2:直線上の一点 #point:距離を計算したい点 u = np.array([line_p2[0] - line_p1[0], line_p2[1] - line_p1[1]]) v = np.array([point[0] - line_p1[0], point[1] - line_p1[1]]) dist = abs(np.cross(u, v) / np.linalg.norm(u)) return dist
参考:
https://tokibito.hatenablog.com/entry/20121227/1356581559
同次連立一次方程式の非自明解を特異値分解から解く
行
列でランク
である行列
と,
次元のベクトル
について,以下の等式が成立するとき,
の非自明解
を特異値分解から求める.
まず,は大きさが不定なので,条件として以下を加える.
ところで,このは以下の解と言いかえることができる.
また,の特異値分解の結果を以下で表す.
図で書くとこう.

はユニタリ行列であり,ユニタリ行列による変換は等長変換であることに注意して,
は以下のように変形できる.
ただし,
以上から,
ここで,の特異値を
とし,
とおくと,
これを最小化する (ただし
)の各成分
は
ここで,の各列をベクトル
と表すと,
がユニタリ行列であるから
参考:
https://www2.cs.duke.edu/courses/fall15/compsci527/notes/linear-systems.pdf
http://daily-tech.hatenablog.com/entry/2018/03/18/180439
ScipyのLevenberg-Marquardt法で大域的最適解に落ちるか試した(だけ)
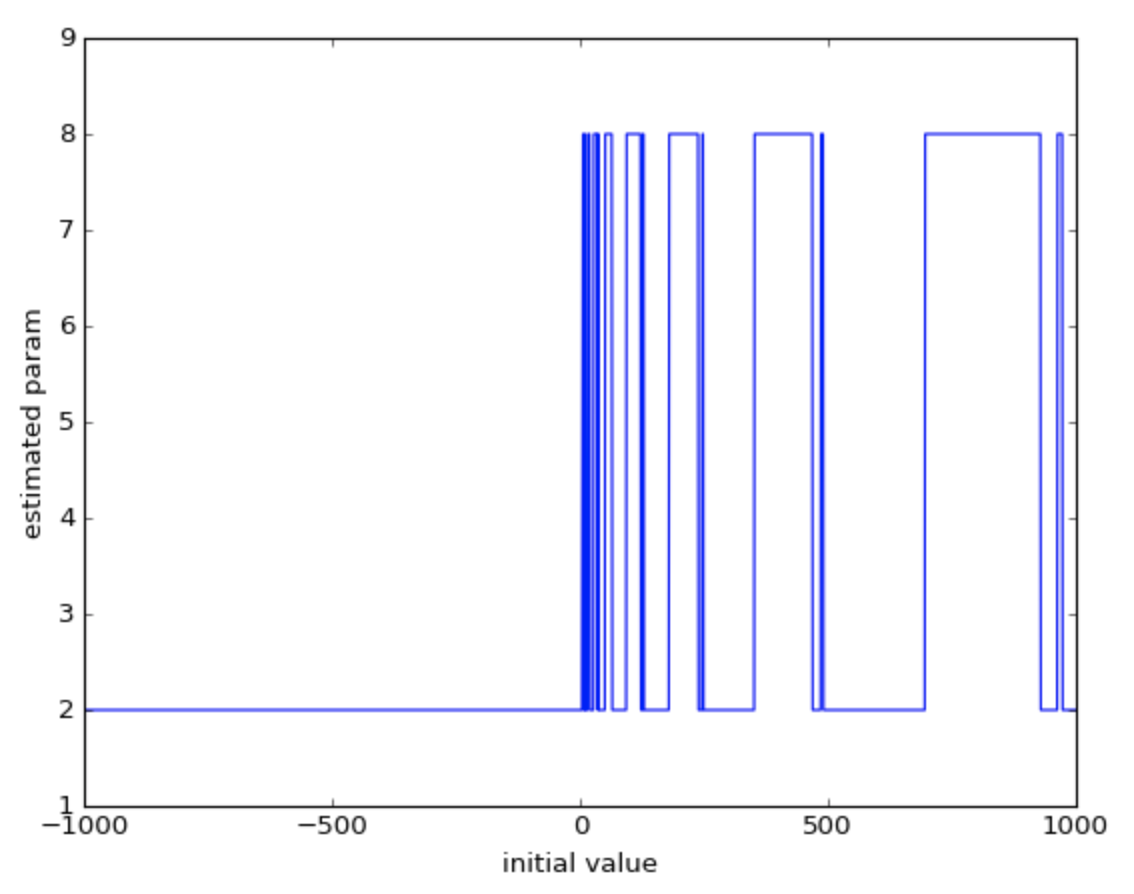
scipy.optimize.least_squaresライブラリを使ってLevenberg-Marquardt法を試しました.
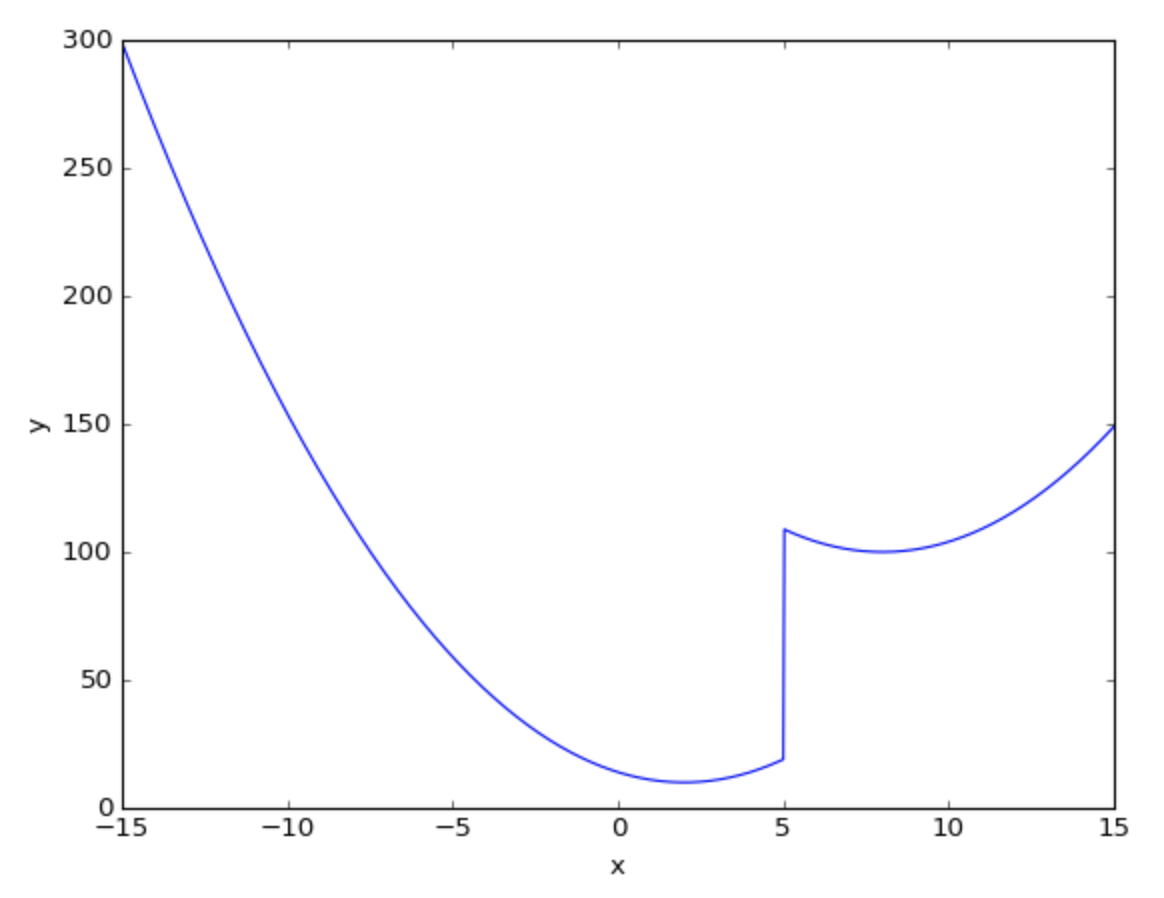
局所最適解はx=8, 大域的最適解はx=2.
深い考察はありません.
from scipy.optimize import least_squares import numpy as np from matplotlib import pylab as plt ### 関数 def func(param): if param>5: funcval= (param-8)**2+100 else: funcval= (param-2)**2+10 return funcval data = np.ones(1000) x = np.linspace(-15,15,1000) for i in range(0,1000): data[i] = func(x[i]) plt.figure() plt.plot(x,data) plt.ylabel("y") plt.xlabel("x") plt.show() ###どの初期値から始めても大域的最適解に収束するか? data = [] #設定 jac='2-point' bounds=(-np.inf, np.inf) method='lm' for i in range(-1000,1000): param = i result = least_squares(func,param,jac,bounds,method) data.append([i,result.x[0]]) data = np.array(data) plt.figure() plt.plot(data[:,0],data[:,1]) plt.ylabel("estimated param") plt.xlabel("initial value") plt.show()
関数の形状
初期値と推定解